MÉTODO MATEMÁTICO PARA CALCULAR UNA REGRESIÓN CUADRÁTICA PARA DETERMINAR LA TENDENCIA DE LAS EMISIONES DE CO₂E EN CATALUÑA.
Introducción.
Para calcular la evolución de las emisiones más allá de 2023, como se explica en el post “Transición Energética en Cataluña: Una mirada al histórico de emisiones de CO₂e de los últimos 34 años”, se ha considerado apropiado utilizar el método de la regresión cuadrática para analizar las tendencias de emisiones de gases de efecto invernadero modelándolas en tres períodos diferentes (1990-2023, 2014-2023 y 2019-2023) para los cuales se dispone de datos reales de emisiones totales. Estos datos provienen de las mediciones de emisiones de gases de efecto invernadero reportadas por EDGAR (Emissions Database for Global Atmospheric Research), accesibles en el siguiente enlace:
https://edgar.jrc.ec.europa.eu/dataset_ghg2024_nuts2
Para analizar las emisiones en Cataluña, se seleccionaron los datos específicos de esta región de la base de datos EDGAR. Esta base de datos incluye las emisiones de varios gases de efecto invernadero: CO₂ (dióxido de carbono) de fuentes fósiles, CH₄ (metano), N₂O (óxido nitroso) y gases F (gases fluorados). Sumando las emisiones anuales de cada gas y expresándolas en términos de equivalentes totales de CO₂ (en kilotoneladas), se obtiene el total de gases de efecto invernadero generados anualmente en Cataluña entre 1990 y 2023. Es importante señalar que a este total anual le faltaría añadir una pequeña cantidad adicional correspondiente a las emisiones secundarias anuales de algunos gases de efecto invernadero no registrados por EDGAR. La base de datos EDGAR (Emissions Database for Global Atmospheric Research) se centra en los principales gases de efecto invernadero regulados por el Protocolo de Kioto, pero no cubre de manera exhaustiva todos los posibles gases de efecto invernadero.
Por lo tanto, a partir de los datos anuales de emisiones de CO₂e, se genera el Gráfico 1. En él, se puede ver claramente cómo han evolucionado estas emisiones a lo largo del período 1990-2023. Este gráfico nos ha servido como punto de partida para analizar en profundidad las tendencias futuras de emisiones en Cataluña a partir de 2024.

Un aspecto importante del tratamiento de los datos mencionado en el artículo es que, para llevar a cabo un análisis exhaustivo, es necesario eliminar el dato correspondiente al año 2020, ya que ese año, marcado por la pandemia de COVID-19, presenta una caída anómala en las emisiones. Incluir este valor podría generar un sesgo significativo en los cálculos y afectar los resultados de la tendencia de emisiones futuras.
Como se puede ver claramente en el Gráfico 1, los datos muestran un comportamiento no lineal de las emisiones de CO₂e a lo largo de los últimos 34 años. En este contexto, como ya se comentó anteriormente, para estimar las emisiones en los próximos años, dadas las características de este pequeño estudio, realizar una regresión cuadrática con los datos de emisiones anuales de CO₂e es una opción adecuada para modelar el sistema y estimar la evolución de las emisiones en los próximos años.
Método de Cálculo de una Regresión Cuadrática
La regresión cuadrática es un método estadístico ampliamente utilizado por su simplicidad para encontrar una relación entre dos variables: una variable independiente X (en este caso, los años) y una variable dependiente Y (las emisiones de CO₂e). Este método es muy útil para predecir comportamientos, especialmente cuando la relación no es lineal, sino que sigue una forma de curva. Es una herramienta estadística simple pero muy potente para analizar datos con comportamientos no lineales, y es especialmente útil cuando se quiere capturar patrones complejos y entender mejor las tendencias sin entrar en modelos multivariables más complejos.
Para realizar una regresión cuadrática con los datos disponibles, se busca ajustar estos datos a una función en forma de parábola que mejor se ajuste a los datos y minimice el error entre los valores reales y los valores predichos por el modelo. Esto se logra mediante el método de los mínimos cuadrados, que calcula los coeficientes (a, b y c) de la ecuación parabólica de la regresión cuadrática, garantizando que la diferencia total entre los valores reales de los datos y los valores predichos (error) sea la menor posible.
La ecuación parabólica de una regresión cuadrática está representada por la siguiente ecuación:

Objetivo del Método de Regresión Cuadrática


Paso 1: Procedimiento para Calcular la Regresión Cuadrática
El método utilizado para ajustar el modelo es el de los mínimos cuadrados, que consiste en encontrar los coeficientes a, b y c de la ecuación parabólica que minimizan la suma de los cuadrados de los residuos. Esto significa que el modelo debe hacer que el error global sea lo más pequeño posible.
El primer paso es definir lo que se llama la función de costo, que es la suma de los cuadrados de los residuos de todos los datos del modelo, es decir:
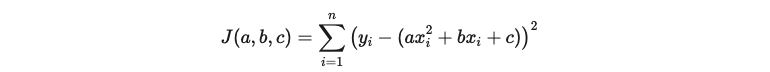
Esta función J(a, b, c) tiene como objetivo calcular cómo el modelo se ajusta a los datos reales. En otras palabras, busca encontrar los valores de los coeficientes a, b y c que hacen que la función de costo J(a, b, c) sea mínima y, por lo tanto, definen de la mejor manera la curva cuadrática que más se asemeja a los datos reales. Para lograr esto, es necesario derivar la función de costo respecto a cada uno de los coeficientes de la ecuación parabólica e igualar estas derivadas a cero. Esto genera un sistema de ecuaciones que se puede resolver de la siguiente manera:


Partiendo de la ecuación de regresión cuadrática:

Una vez establecido el sistema matricial, el siguiente paso es determinar, mediante cálculo matricial, cuáles son los valores óptimos de los coeficientes a, b y c que minimizan el error entre los valores observados y los predichos por el modelo.


Una vez determinado que la matriz (XTX)-1 es invertible1, y posteriormente resuelto este sistema mediante cálculo matricial, se obtienen directamente los valores óptimos de los coeficientes a, b y c que minimizan el error, como se explicó al principio:

Que, a efectos prácticos, en nuestro caso, para el análisis de emisiones de CO₂e a lo largo del tiempo, esto significa que:

Paso 2: Procedimiento de validación de los resultados obtenidos para asegurarse de que los modelos se ajustan adecuadamente a los datos reales.
Una vez calculados los modelos de regresión cuadrática, es imprescindible validar los resultados para asegurarse de que estos modelos encontrados se ajustan adecuadamente a los datos reales. Esta validación es clave para determinar con un cierto grado de confianza si los modelos son adecuados y pueden ser utilizados para hacer predicciones fiables. Para ello, se utilizan dos métodos: el coeficiente de determinación (R²) y la raíz del error cuadrático medio (RMSE).
R² y RMSE son dos métodos ampliamente utilizados en estadística para evaluar la calidad de un modelo matemático. R² (coeficiente de determinación) indica qué parte de la variabilidad de los datos reales es explicada por el modelo. Un valor cercano a 1 significa que el modelo explica muy bien los datos, mientras que un valor cercano a 0 indica que hay poca relación entre el modelo y los datos reales. En cambio, el RMSE (Root Mean Squared Error), mide, en promedio, el error del modelo en sus predicciones. Expresado en las mismas unidades que los datos, el RMSE muestra hasta qué punto las predicciones del modelo se alejan de los valores reales.
En otras palabras, R² nos ayuda a entender «qué tan bien el modelo explica los datos reales», mientras que el RMSE nos indica «qué tan precisas son sus predicciones». Para asegurarse de que los modelos se ajustan a la realidad y pueden predecir con cierta credibilidad las tendencias de emisiones de CO₂e en los próximos años, es necesario obtener un R² alto y un RMSE bajo.
Para calcular estos dos parámetros, se debe seguir el siguiente procedimiento:


- Que una matriz sea invertible significa que existe otra matriz, llamada matriz inversa, que al multiplicarse por la matriz original da como resultado la matriz identidad. Esta propiedad es fundamental en álgebra lineal y tiene importantes implicaciones en la resolución de sistemas de ecuaciones lineales, entre otras aplicaciones.


↩︎