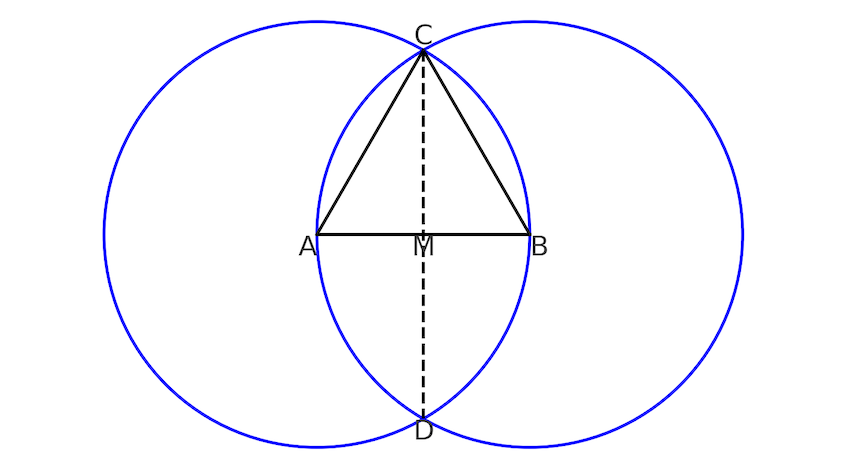
La géométrie de base du gothique : la vesica piscis.
Les cathédrales gothiques sont une synthèse parfaite de l’ingéniosité humaine, de la beauté de la géométrie et de la spiritualité. Elles témoignent d’une époque où le savoir et la foi se sont unis pour créer, à travers l’architecture, une connexion entre le monde terrestre et le royaume céleste. En entrant dans ces espaces, nous nous immergeons dans un univers où chaque proportion, chaque angle et chaque forme fait partie d’un langage géométrique qui exprime la quête de l’infini et le désir d’atteindre le ciel. Tout semble conçu pour impressionner : les voûtes élancées, les vitraux colorés et les détails décoratifs nous font sentir petits et, en même temps, partie intégrante de quelque chose d’immense. Cette architecture en pierre est un exploit du talent humain, présent dans chaque recoin. Mais ce qui est le plus fascinant, ce sont les moyens techniques et les connaissances utilisés pour construire ces merveilles de l’architecture et de l’ingénierie. À l’aube de l’ère gothique, une époque où les chiffres romains étaient encore utilisés pour le commerce, tandis que les chiffres arabes, beaucoup plus pratiques pour les calculs et l’algèbre, étaient presque inconnus en Europe, les grandes cathédrales gothiques ont été principalement construites selon des principes géométriques que les élèves des premières années de collège étudient encore aujourd’hui.
Ainsi, il n’est pas exagéré de dire que les cathédrales gothiques, par leur majesté architecturale et, en même temps, l’élégance des concepts géométriques qui les ont inspirées, sont un exemple impressionnant de la manière dont l’ingéniosité humaine, la beauté de la géométrie et la spiritualité peuvent s’unir pour créer quelque chose d’extraordinaire. Les cathédrales ne sont pas de simples bâtiments : elles sont le symbole d’une époque où le savoir et la religion collaboraient pour connecter le monde terrestre et le ciel. En pénétrant dans ces espaces, tout semble pensé pour nous émerveiller : les voûtes élevées, les vitraux colorés et les détails décoratifs nous font nous sentir petits et, par ailleurs, partie intégrante de quelque chose de bien plus grand. Mais, ce qui est le plus fascinant, c’est la manière dont ces merveilles ont été construites à une époque où les outils modernes et les calculs mathématiques que nous utilisons aujourd’hui n’existaient pas.
Pour comprendre la géométrie qui se cache derrière ces constructions colossales, nous devons partir d’une des formes géométriques les plus élémentaires : le triangle équilatéral, symbole du christianisme médiéval associé à la Trinité (Père, Fils et Saint-Esprit), représentant l’unité dans la diversité. Cependant, pour le construire à partir de la règle et du compas, comme le faisaient les maîtres bâtisseurs du Moyen Âge, il est nécessaire de passer d’abord par une autre figure, qui est l’un des symboles les plus puissants du christianisme et la base de nombreux éléments de l’architecture gothique : la vesica piscis. La vesica piscis est une figure géométrique créée par l’intersection de deux cercles de même rayon, où le centre de chaque cercle se trouve sur la circonférence de l’autre. Cette forme, qui ressemble à un poisson selon certaines interprétations, a été adoptée par le christianisme primitif, mais existait déjà sous d’autres noms et avec d’autres significations dans des civilisations antérieures comme les cultures mésopotamiennes, africaines et asiatiques.
Cette figure, le poisson, est devenue un symbole secret d’identité et de foi pour les chrétiens comme collectif durant les premiers siècles de persécution dans l’Empire romain. Ce symbole provient du mot grec « ἰχθύς » (ichthys), qui signifie « poisson » et se décompose en un acronyme :
- CH: « Christos » (Crist)
- I: « Iesous » (Jésus)
- TH: « Theou » (de Dieu)
- Y: « Yios » (Fils)
- S: « Soter » (Sauveur)
Cet acronyme était une manière de coder l’essence du christianisme en seulement quelques caractères, et il devint l’un des symboles les plus reconnaissables et puissants de l’iconographie chrétienne. Ichthys était lors des premiers siècles du christianisme (1,2 et 3 siècles), l’équivalent des sigles modernes que nous utilisons aujourd’hui pour condenser des concepts ou identifier des institutions à l’aide des initiales des mots les plus importants. Pour les premiers chrétiens, ichthys n’était pas simplement un mot, mais un message intrinsèquement puissant et profondément symbolique, qui encapsulait en cinq lettres les croyances fondamentales de leur foi. Et, en accompagnant cet acronyme, il y avait un « logotype » parfait : la vesica piscis, une forme mystique d’intersection évoquant l’image d’un poisson, qui deviendra le symbole iconique du christianisme. Ainsi, on pourrait dire qu’ichthys fut un exemple impeccable de branding, créé avec brio par les premiers chrétiens pour identifier et façonner leur foi.
Il est fascinant d’observer comment la vesica piscis, un symbole profondément enraciné dans l’iconographie chrétienne, devient la figure géométrique essentielle dans la construction des cathédrales. Loin d’être simplement un ornement, cette figure apporte une proportion mathématique remarquable, conférant aux constructions gothiques une harmonie et une beauté incomparables, devenant ainsi le modèle géométrique omniprésent dans les proportions de nombreux éléments de ces édifices.
Pour mieux comprendre cette harmonie, observons le graphique suivant..
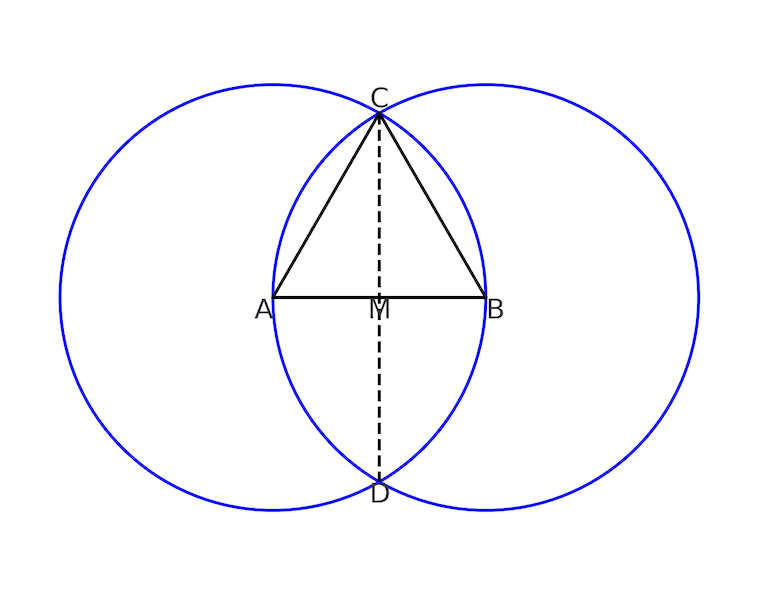
Dans celui-ci, on peut voir comment, à l’intersection de deux circonférences, apparaît un triangle équilatéral parfaitement inscrit dans la vesica piscis. À partir de celui-ci, et du théorème de Pythagore, on peut facilement calculer les proportions de cette figure. Comme le montre le diagramme du graphique précédent, le triangle (ABC) est équilatéral et se trouve exactement au centre de la vesica piscis. En prenant (AB = 1), la distance (AM) devient 1/2.
Avec ces valeurs et en appliquant le théorème de Pythagore, on peut calculer la longueur de (CM) :
Ainsi, la longueur totale de (CD) est le double de (CM), c’est-à-dire,
Par conséquent, le rapport entre la longueur et la largeur de la vesica piscis peut s’exprimer mathématiquement comme suit :
En obtenant que la racine carrée de 3, un nombre irrationnel, est le rapport entre la longueur et la largeur de la vesica piscis.
Les maîtres d’œuvre médiévaux ont utilisé la vesica piscis comme base pour établir les proportions des éléments les plus importants des cathédrales gothiques. Cette figure géométrique se retrouve dans les arcs brisés, les voûtes sur croisée d’ogives, les nefs, les fenêtres et les rosaces, entre autres. Elle apportait non seulement une beauté visuelle, mais encore une harmonie et un équilibre structurel, transformant ces constructions en véritables chefs-d’œuvre.
Dans ce sens, l’élément gothique le plus connu de tous, l’arc brisé, peut facilement être identifié à l’intérieur de la vesica piscis si l’on observe la figure formée par les points A, B et C à l’intersection des deux cercles. Cette forme pointue des arcs n’est pas uniquement esthétique ; l’arc brisé remplit une fonction structurelle essentielle. Contrairement aux arcs en plein cintre de l’architecture romane, qui « poussent » les forces vers les côtés et nécessitent des murs épais pour résister à ces forces latérales, l’arc brisé a permis aux maîtres bâtisseurs de diriger le poids de tous les éléments verticalement vers le bas, jusqu’aux bases de l’arc. Cela a rendu possible la construction de structures plus hautes et plus élancées sans avoir besoin de contreforts latéraux massifs.
Ce design repose sur une répartition des forces modélisée par l’équation mathématique que nous écririons aujourd’hui comme :
où F représente la force qui se déplace vers le bas, W est la charge supportée par l’arc (c’est-à-dire le poids de la voûte ou du toit), et theta est l’angle de l’arc brisé. En redirigeant le poids vers les bases, les bâtisseurs médiévaux ont pu créer des espaces lumineux grâce à des murs hauts et légers dotés de grandes ouvertures pour les vitraux. Ce jeu de forces a doté les cathédrales européennes d’une innovation technique pour l’époque, défiant presque la gravité.
Cependant, aussi techniquement avancé que ce type de construction semble pour l’époque, il faut tenir compte d’un détail fondamental qui ne peut pas être ignoré : les maîtres bâtisseurs de l’époque ne disposaient pas de calculs algébriques ni d’équations comme celles présentées dans cet article pour construire les cathédrales gothiques. Ils ne possédaient ni les outils modernes ni les connaissances mathématiques avancées que nous considérons aujourd’hui comme indispensables pour mener à bien un projet de construction. Ce qu’ils possédaient, en revanche, était une profonde connaissance pratique, fruit de l’expérience accumulée et transmise de génération en génération. Cette expérience leur permettait de comprendre avec une grande précision comment fonctionnaient les forces et la répartition du poids dans leurs constructions colossales, obtenant des résultats qui continuent de nous fasciner des siècles plus tard.
Dans ce sens, il faut se rappeler que, bien que la trigonométrie — la branche des mathématiques qui étudie les angles et les distances — était déjà connue par des cultures anciennes comme les Babyloniens, en Europe au XIIᵉ siècle, au début de la période gothique, on venait à peine de découvrir l’existence du chiffre zéro. Les calculs étaient encore réalisés avec les chiffres romains. Quelles sont les implications ? Cela signifie que les maîtres bâtisseurs ne pouvaient pas concevoir la structure des cathédrales sur la base d’estimations numériques, car les chiffres romains n’étaient pas pratiques pour effectuer des calculs complexes comme ceux nécessaires à la construction. Pour voir un progrès dans ce domaine, il faut avancer jusqu’au XIIIᵉ siècle. À cette époque, le mathématicien de renom italien Leonardo Fibonacci rédige son Liber Abaci (1202), avec pour objectif d’introduire et de populariser en Europe le système de numération indo-arabe, qui utilise les chiffres de 0 à 9 et le concept du zéro, tel que nous l’utilisons aujourd’hui comme base pour les calculs. Ce système était bien plus pratique pour les calculs et la trigonométrie que le système de numération romain, qui, comme mentionné, dominait encore en Europe à l’époque, mais était moins efficace. Toutefois, il faudra encore des siècles avant que ces méthodes de calcul soient généralisées dans tous les domaines de la société, y compris dans le champ de l’architecture et de la construction en Europe.
Un autre élément caractéristique du style gothique, les voûtes d’ogives des nefs, élément fondamental de la structure des cathédrales gothiques, repose également sur la vesica piscis comme élément clé de sa conception. Formées par l’intersection d’arcs brisés, ces voûtes créent un réseau de lignes qui distribue le poids avec précision, grâce à le principe des surfaces réglées. Les maîtres d’œuvre gothiques réalisaient méticuleusement chaque nervure pour garantir que la voûte supportait le poids sans compromettre la stabilité de l’édifice.
Concernant les fenêtres à vitraux et les rosaces des cathédrales gothiques, ces éléments constituent également de magnifiques exemples visuels de la manière dont la vesica piscis est devenue une base fondamentale en même temps pour les proportions et pour les motifs décoratifs. Cette figure géométrique n’est pas seulement présente et influence les dimensions générales de ces éléments, mais elle se manifeste également dans les motifs complexes que l’on trouve à l’intérieur de ces derniers. Les maîtres d’œuvre et les artisans verriers de l’époque ont développé une habileté impressionnante, compte tenu des moyens de l’époque, en créant des cercles tangents, des polygones réguliers et des figures étoilées à l’intérieur, combinant avec précision le verre et la pierre pour donner vie à ces chefs-d’œuvre. La complexité de ces motifs reflète une connaissance approfondie de la géométrie et une capacité technique extraordinaire. À propos de ce sujet, des fenêtres et des rosaces des cathédrales gothiques, en raison de leur complexité et du grand nombre de détails qu’elles présentent, je parlerai dans une autre publication pour offrir une explication posée et détaillée sur la relation entre les proportions, la géométrie des ornements de ces éléments et la vesica piscis.
À une époque sans calculs complexes ni outils modernes, les maîtres d’œuvre ont érigé ces structures colossales avec de la géométrie, de l’intuition et des connaissances transmises de génération en génération. La géométrie n’était pas seulement une ressource technique, mais également une manière de se connecter au divin. Parmi toutes les figures géométriques qui soutiennent cet héritage, la vesica piscis se distingue comme un symbole d’harmonie et de transcendance. Cette figure, créée, comme nous l’avons vu, par l’intersection de deux cercles de rayons identiques, où le périmètre de chacun passe par le centre de l’autre, est devenue non seulement un emblème spirituel, mais encore la base pour concevoir les proportions et les formes d’éléments clés des cathédrales, comme les arcs brisés, les voûtes d’ogives, les fenêtres et les rosaces, entre autres. La vesica piscis, avec le triangle équilatéral en son intérieur, nous rappelle comment la beauté inhérente de la géométrie peut être en même temps fonctionnelle et symbolique. Ce symbole, qui unit mysticisme et précision technique, reflète la riche interconnexion du Moyen Âge entre la science et la foi, entre l’homme et le divin. Les cathédrales gothiques, par conséquent, ne sont pas seulement des édifices imposants, mais de véritables œuvres d’art qui intègrent des connaissances mathématiques, philosophiques et spirituelles. Elles nous rappellent la capacité de l’humanité à comprendre et à donner forme à ce qui semble impossible. Cet héritage architectural continue d’inspirer et d’émerveiller ceux qui les contemplent, offrant une fenêtre sur une époque où les mathématiques et la géométrie étaient considérées comme une voie pour comprendre le cosmos et sa beauté inhérente.