MÉTHODE MATHÉMATIQUE POUR CALCULER UNE RÉGRESSION QUADRATIQUE POUR DÉTERMINER LA TENDANCE DES ÉMISSIONS DE CO₂E EN CATALOGNE.
Introduction.
Pour calculer l’évolution des émissions au-delà de 2023, comme expliqué dans le post « Transition Énergétique en Catalogne : Un regard sur l’historique des émissions de CO₂e des 34 dernières années », il a été jugé approprié d’utiliser la méthode de la régression quadratique pour analyser les tendances des émissions de gaz à effet de serre en les modélisant sur trois périodes différentes (1990-2023, 2014-2023 et 2019-2023) pour lesquelles des données réelles sur les émissions totales sont disponibles. Ces données proviennent des mesures des émissions de gaz à effet de serre rapportées par EDGAR (Emissions Database for Global Atmospheric Research), accessibles via le lien suivant :
https://edgar.jrc.ec.europa.eu/dataset_ghg2024_nuts2
Pour analyser les émissions en Catalogne, les données spécifiques à cette région ont été sélectionnées dans la base de données EDGAR. Cette base de données comprend les émissions de divers gaz à effet de serre : CO₂ (dioxyde de carbone) provenant de sources fossiles, CH₄ (méthane), N₂O (protoxyde d’azote) et les gaz F (gaz fluorés). En additionnant les émissions annuelles de chaque gaz et en les exprimant en termes d’équivalent CO₂ total (en kilotonnes), on obtient le total des gaz à effet de serre générés chaque année en Catalogne de 1990 à 2023. Il convient de noter que ce total annuel manque d’une petite quantité supplémentaire correspondant aux émissions secondaires annuelles d’une série de gaz à effet de serre non enregistrés par EDGAR. La base de données EDGAR (Emissions Database for Global Atmospheric Research) se concentre sur les principaux gaz à effet de serre réglementés par le Protocole de Kyoto, mais ne couvre pas de manière exhaustive tous les gaz à effet de serre possibles.
Ainsi, à partir des données annuelles sur les émissions de CO₂e, le Graphique 1 est généré. Dans ce graphique, on peut voir l’évolution de ces émissions sur la période 1990-2023. Ce graphique a servi de point de départ pour analyser en profondeur les tendances futures des émissions en Catalogne à partir de 2024.

Un aspect important du traitement des données mentionné dans l’article est que, pour réaliser une analyse approfondie, nous devons éliminer la donnée pour l’année 2020, car cette année, marquée par la pandémie de COVID-19, présente une baisse anormale des émissions. Inclure cette valeur pourrait entraîner un biais significatif dans les calculs et affecter les résultats de la tendance des émissions futures.
Comme on peut clairement le voir dans le Graphique 1, les données montrent une tendance non linéaire des émissions de CO₂e lors des 34 dernières années. Dans ce contexte, comme mentionné précédemment, pour estimer les émissions des prochaines années, étant donné les caractéristiques de cette petite étude, effectuer une régression quadratique avec les données des émissions annuelles de CO₂e est une option appropriée pour modéliser le système et estimer l’évolution des émissions dans les années à venir.
Méthode de Calcul d’une Régression Quadratique
La régression quadratique est une méthode statistique largement utilisée pour sa simplicité à trouver une relation entre deux variables : une variable indépendante X (dans ce cas, les années) et une variable dépendante Y (les émissions de CO₂e). Cette méthode est très utile pour prédire des comportements, notamment lorsque cette relation n’est pas linéaire, mais suit une forme courbe. C’est un outil statistique simple, mais puissant pour analyser des données avec des tendances non linéaires et il est particulièrement utile pour capter des schémas complexes et mieux comprendre les tendances sans recourir à des modèles multivariables plus complexes.
Pour effectuer une régression quadratique avec les données disponibles, l’objectif est de les ajuster à une fonction sous la forme d’une parabole qui s’adapte le mieux aux données et minimise l’erreur entre les valeurs réelles et les valeurs prédites par le modèle. Cela est réalisé par la méthode des moindres carrés, qui calcule les coefficients (a, b, et c) de l’équation de la régression quadratique en garantissant que la différence totale entre les valeurs réelles des données et les valeurs prédites (erreur) est minimisée.
L’équation parabolique d’une régression quadratique est représentée par l’équation suivante :

Objectif de la Méthode de Régression Quadratique


Étape 1 : Procédure pour Calculer la Régression Quadratique
La méthode utilisée pour ajuster le modèle est celle des moindres carrés, qui consiste à trouver les coefficients a, b, et c de l’équation parabolique qui minimisent la somme des carrés des résidus. Cela signifie que le modèle doit viser à minimiser l’erreur globale.
La première étape est de définir ce que l’on appelle la fonction de coût, qui est la somme des carrés des résidus de toutes les données du modèle, c’est-à-dire :
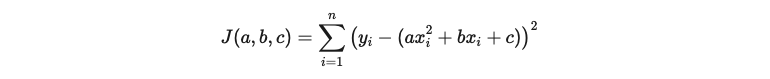
Cette fonction J(a, b, c) vise à calculer comment le modèle s’ajuste aux données réelles. En d’autres termes, elle cherche à trouver les valeurs des coefficients a, b, et c qui rendent la fonction de coût J(a, b, c) minimale et qui, par conséquent, définissent au mieux la courbe quadratique qui correspond le plus aux données réelles. Pour cela, nous devons dériver la fonction de coût par rapport à chaque coefficient de l’équation parabolique et d’égaliser ces dérivées à zéro. Cela génère un système d’équations qui peut être résolu comme suit :

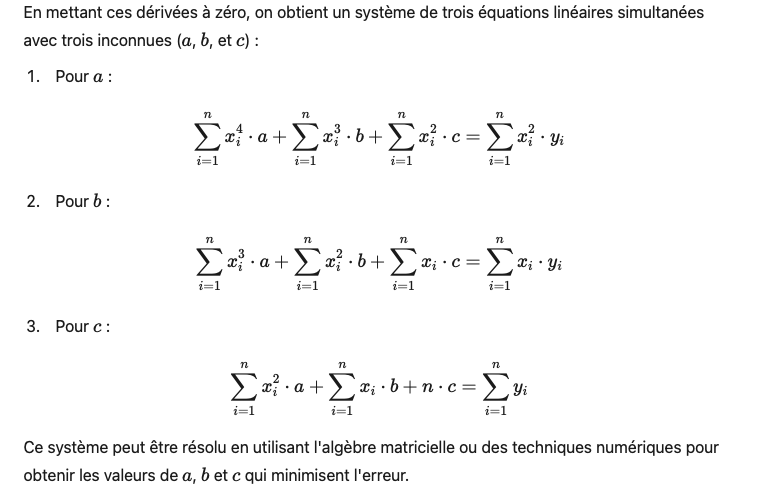
À partir de l’équation de régression quadratique :

Une fois le système matriciel établi, l’étape suivante est de déterminer, par calcul matriciel, les valeurs optimales des coefficients a, b, et c qui minimisent l’erreur entre les valeurs observées et celles prédites par le modèle.


Une fois qu’il a été déterminé que la matrice (XTX)-1 est inversible1, et après avoir résolu ce système par calcul matriciel, on obtient directement les valeurs optimales des coefficients a, b, et c qui minimisent l’erreur, comme expliqué au début :

À des fins pratiques, dans notre cas, pour l’analyse des émissions de CO₂e au fil du temps, cela signifie que :

Étape 2 : Procédure de validation des résultats obtenus pour s’assurer que les modèles s’ajustent de manière adéquate aux données réelles
Une fois les modèles de régression quadratique calculés, il est essentiel de valider les résultats pour s’assurer que ces modèles trouvés s’ajustent de manière adéquate aux données réelles. Cette validation est essentielle pour déterminer avec un certain degré de confiance si les modèles sont appropriés et peuvent être utilisés pour des prédictions fiables. À cette fin, deux méthodes sont utilisées : le coefficient de détermination (R²) et la racine de l’erreur quadratique moyenne (RMSE).
R² et RMSE sont deux méthodes largement utilisées en statistique pour évaluer la qualité d’un modèle mathématique. R² (coefficient de détermination) indique quelle part de la variabilité des données réelles est expliquée par le modèle. Une valeur proche de 1 signifie que le modèle explique bien les données, tandis qu’une valeur proche de 0 indique une faible relation entre le modèle et les données réelles. En revanche, le RMSE (Root Mean Squared Error) mesure, en moyenne, l’erreur de prédiction du modèle. Exprimé dans les mêmes unités que les données, le RMSE montre à quel point les prédictions du modèle s’éloignent des valeurs réelles.
En d’autres termes, R² nous aide à comprendre « à quel point le modèle explique bien les données réelles », tandis que le RMSE indique « à quel point les prédictions sont précises ». Pour s’assurer que les modèles correspondent à la réalité et peuvent prédire de manière fiable les tendances des émissions de CO₂e dans les années à venir, nous devons obtenir un R² élevé et un RMSE faible.
Pour calculer ces deux paramètres, la procédure suivante doit être suivie :


- Qu’une matrice soit inversible signifie qu’il existe une autre matrice, appelée matrice inverse, qui, lorsqu’elle est multipliée par la matrice d’origine, donne la matrice identité. Cette propriété est fondamentale en algèbre linéaire et a des implications importantes dans la résolution de systèmes d’équations linéaires, entre autres applications.


↩︎