Mètode matemàtic per calcular una regressió quadràtica per determinar la tendència de les emissions de CO₂e a Catalunya.
Introducció.
Per calcular l’evolució de les emissions més enllà de 2023, tal com he explicat en el post “Transició Energètica a Catalunya: Una mirada a l’històric d’emissions de CO₂e dels darrers 34 anys“, he cregut convenient utilitzar el mètode de la regressió quadràtica per analitzar les tendències d’emissions de gasos d’efecte hivernacle a partir de la modelització d’aquestes en tres períodes diferents (1990-2023, 2014-2023 i 2019-2023) dels quals disposem de dades reals d’emissions totals que provenen de les mesures d’emissions de gasos d’efecte hivernacle reportades per l’EDGAR (Emissions Database for Global Atmospheric Research), i que estan disponibles en aquest enllaç:
https://edgar.jrc.ec.europa.eu/dataset_ghg2024_nuts2
Per analitzar les emissions a Catalunya, he seleccionat les dades específiques d’aquesta regió de la base de dades EDGAR. Aquesta base inclou emissions de diversos gasos d’efecte hivernacle: el CO₂ (diòxid de carboni) procedent de fonts fòssils, el CH₄ (metà), el N₂O (òxid nitrós) i els gasos F (gasos fluorats). Sumant les emissions anuals de cada gas i expressant-les en termes d’emissions totals equivalents de CO₂e (en kilotones), s’obté el total de gasos d’efecte hivernacle generat anualment a Catalunya entre 1990 i 2023. Cal assenyalar, que a aquest total anual, li faltaria afegir una petita quantitat addicional que correspondria a les emissions secundàries anuals d’una sèrie de gasos d’efecte hivernacle dels quals l’EDGAR no en registra les emissions. La base de dades EDGAR (Emission Database for Global Atmospheric Research) se centra en els principals gasos d’efecte hivernacle regulats pel Protocol de Kyoto, però no cobreix de manera exhaustiva tots els possibles gasos d’efecte hivernacle.
Així doncs, a partir de les dades anuals d’emissions de CO₂e anual, sorgeix el Gràfic 1. En ell, es pot veure clarament com han evolucionat aquestes emissions al llarg del període 1990-2023. Aquest gràfic és el que ens ha servit com a punt de partida per analitzar en profunditat les tendències futures d’emissions a Catalunya a partir del 2024.

Un aspecte importat del tractament de les dades que s’ha esmentat a l’article, és el fet que s’ha considerat que per poder dur a terme una anàlisi acurada de les dades, és necessari eliminar la dada corresponent a l’any 2020, ja que aquell any, marcat per la pandèmia de la COVID-19, presenta una caiguda anòmala en les emissions. Incloure aquest valor, podria generar un biaix significatiu en els càlculs i afectar el resultat de tendència d’emissions futures.
Com es pot veure clarament al Gràfic 1, les dades mostren un comportament de les emissions de CO₂e al llarg dels darrers 34 anys clarament no lineal. En aquest context, tal com ja he comentat a l’inici, per dur a terme l’estimació de les emissions en els pròxims anys, donades les característiques d’aquest petit estudi, realitzar una regressió quadràtica amb les dades d’emissions anuals de CO₂e és una opció adequada per modelar el sistema per tal d’estimar l’evolució de les emissions en els pròxims anys.
Mètode de Càlcul d’una Regressió Quadràtica.
La regressió quadràtica és un mètode estadístic molt utilitzat per la seva simplicitat per trobar una relació entre dues variables, una variable independent X (en aquest cas, els anys) i una variable dependent Y (les emissions de CO₂e). Aquest mètode és molt útil per predir comportaments, especialment quan aquesta relació no és lineal sinó que segueix una forma de corba. Es tracta d’una eina estadística simple, però molt potent, per analitzar dades amb comportaments no lineals i és especialment útil quan volem capturar patrons complexos i entendre millor les tendències, sense entrar en models multivariables més complexos.
Per dur a terme una regressió quadràtica, a partir de les dades del que es disposen del model que s’estudia, es busca ajustar aquestes dades a una funció en forma de paràbola que millor s’ajusti a les dades i que minimitzi l’error entre els valors reals obtinguts i els valors predits pel model. Això s’aconsegueix mitjançant el mètode que s’anomena dels mínims quadrats, que calcula els coeficients (a, b i c) de l’equació parabòlica de la regressió quadràtica que garanteixen que la diferència total entre els valors de les dades reals i els valors predits pel model (error) sigui la més petita possible.
L’equació parabòlica d’una regressió quadràtica està representada per la següent equació:

Objectiu del mètode de regressió quadràtica


Pas 1: Procediment de càlcul de la regressió quadràtica
El mètode utilitzat per ajustar el model és el dels mètodes dels mínims quadrats, que consisteix a trobar els coeficients a, b, i c de l’equació parabòlica que minimitzen la suma dels quadrats dels residus. Això significa que el model que es busca ha de fer que l’error global sigui el més petit possible.
El primer pas és el de definir el que s’anomena la funció de cost, que és la suma dels quadrats dels residus de totes les dades del model, és a dir:
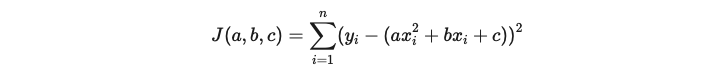
Aquesta funció J(a,b,c) el seu objectiu és el de calcular com el model s’ajusta les dades reals. En altres paraules, trobar els valors dels coeficients a, b, i c que fan que la funció de cost J(a,b,c) sigui mínima i que, per tant, siguin aquests els que millor defineixen la corba quadràtica que coincideixi al màxim amb les dades reals. I per això, és necessari derivar la funció de cost respecte a cadascun dels coeficients de l’equació parabòlica i igualar les derivades a zero. Això genera un sistema d’equacions que es pot resoldre de la següent manera:

Quan s’igualen aquestes derivades a zero, s’obté un sistema de tres equacions lineals simultànies amb tres incògnites (a, b, i c) el qual es pot resoldre de manera més eficient transformant les equacions algebraiques a la seva forma matricial, que és una metodologia de resolució especialment útil quan hi ha moltes dades i que el seu procediment de càlcul és el següent:
Partint de l’equació de regressió quadràtica, que és:

Un cop tenim el sistema matricial establert, el següent pas és el de trobar, mitjançant càlcul matricial quins són els valors òptims dels coeficients a, b, i c que minimitzen l’error entre la diferència dels valors observats i els predits pel model.



Un cop determinat que la matriu (XTX)-1 és invertible1, i posteriorment s’ha resolt aquest sistema mitjançant càlcul matricial, obtenim directament els valors òptims dels coeficients a, b, i c que minimitzen l’error, on com s’ha explicat al principi:

Que a efectes pràctics en el nostre cas, per l’anàlisi d’emissions de CO₂e al llarg del temps, significa que:

Pas 2: Procediment de validació dels resultats obtinguts per assegurar que els models s’ajusten adequadament a les dades reals.
Un cop calculats els models de regressió quadràtica, és imprescindible validar els resultats per assegurar que aquests models trobats s’ajusten adequadament a les dades reals. Aquesta validació és clau per determinar amb un cert grau de confiança si els models són adequats i poden utilitzar-se per fer prediccions fiables. Per aquesta fi, es fan servir dos mètodes: el del coeficient de determinació (R²) i l’arrel de l’error quadràtic mitjà (RMSE, per les seves sigles en anglès).
El R² i el RMSE són dos mètodes àmpliament utilitzats en estadística per avaluar la qualitat d’un model matemàtic. El R² (coeficient de determinació), indica quina part de la variabilitat de les dades reals és explicada pel model. Un valor proper a 1 significa que el model explica molt bé les dades, mentre que un valor proper a 0 indica que hi ha poca relació entre el model i les dades reals. En canvi, el RMSE (l’Arrel d’Error Quadràtic Mitjà), mesura, de mitjana, l’error del model en les seves prediccions. Expressat en les mateixes unitats que les dades, el RMSE ens mostra fins a quin punt les prediccions del model s’allunyen dels valors reals.
En altres paraules, el R² ens ajuda a entendre “com de bé el model explica les dades reals”, mentre que el RMSE ens indica “com són de precises les seves prediccions”. Per assegurar que els models s’ajusten a la realitat i poden predir amb una certa credibilitat les tendències d’emissions de CO₂e en els pròxims anys, cal aconseguir un R² alt i un RMSE baix.
Així doncs, per calcular aquests dos paràmetres, s’ha de seguir el següent procediment


- Que una matriu sigui invertible significa que existeix una altra matriu, anomenada matriu inversa, que quan es multiplica per la matriu original dona com a resultat la matriu identitat. Aquesta propietat és fonamental en àlgebra lineal i té implicacions importants en la resolució de sistemes lineals d’equacions, entre altres aplicacions.
 ↩︎
↩︎